equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
A intensidade de cada interação é definida pela sua constante de acoplamento, um parâmetro adimensional que serve para comparar as diferentes interações. No caso particular da interação eletromagnética, a constante de acoplamento é obtida a partir da expressão da energia potencial eletrostática entre duas cargas puntiformes divida pelor fator ħc.
A constante de acoplamento da interação eletromagnética é também conhecida como a constante de estrutura fina , já substituindo os valores das constantes. Na tabela a seguir são apresentadas características específicas de cada interação:[
A renormalização é um conjunto de técnicas utilizadas para eliminar os infinitos que aparecem em alguns cálculos em Teoria Quântica de Campos.[1] Na mecânica estatística dos campos[2] e na teoria de estruturas geométricas auto-similares,[3] a renormalização é usada para lidar com os infinitos que surgem nas quantidades calculadas, alterando valores dessas quantidades para compensar os efeitos das suas auto-interações. Inicialmente vista como um procedimento suspeito e provisório por alguns de seus criadores, a renormalização foi posteriormente considerada uma ferramenta importante e auto-consistente em vários campos da física e da matemática. A renormalização é distinta da outra técnica para controlar os infinitos, regularização, que assume a existência de uma nova física desconhecida em novas escalas.[4]
Renormalização em EDQ
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
Os campos e a constante de acoplamento são realmente quantidades "cruas", por isso, o índice B acima. Convencionalmente, as quantidades cruas são escritas de modo que os termos lagrangianos
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
////// correspondentes sejam múltiplos dos renormalizados:
Teoria de gauge e Identidade de Ward-Takahashi[5][6] implicam que podemos renormalizar os dois termos da parte derivada covariante juntos[7], que é o que aconteceu para Z2, é o mesmo com Z1.[8]
Em física, um modelo sigma é um sistema físico[1] que é descrito por uma densidade de Lagrange da forma:
Quebra espontânea de simetria é um processo pelo qual um sistema simétrico passa, de forma espontânea, para um estado não simétrico. Este tipo de processo, incomum na natureza física, é vital para a compreensão do modelo padrão das partículas fundamentais, que é um dos mais importantes ramos da física moderna.
Definição
Para que uma quebra espontânea de simetria ocorra, deve necessariamente haver um sistema no qual existam diversos estados subsequentes com iguais probabilidades de ocorrer. Este sistema, como um todo, então é tratado como um sistema simétrico. Entretanto apenas um dos estados subsequentes deve ocorrer e toda a probabilidade dos inúmeros estados diversos é reduzida a zero, já que não há mais simetria. Então, é dito que a simetria do sistema foi espontaneamente quebrada.
Definição formal
Quando uma teoria é dita simétrica com respeito à um grupo simétrico, mas afirma que um elemento deste grupo é distinto, então uma quebra espontânea de simetria ocorreu, ou seja, pela teoria, não é necessário que se identifique o elemento e sim apenas que haja um elemento distinto.
Importância no modelo padrão
 Ver artigo principal: Mecanismo de Higgs
Ver artigo principal: Mecanismo de HiggsSem a quebra espontânea de simetria o modelo padrão prediz a existência de um determinado número de partículas. Entretanto, algumas destas partículas (os bosões W e Z, por exemplo) são preditos de não possuir massa, quando na realidade eles possuem massa. Esta era a maior falha do modelo até que o físico escocês Peter Higgs e outros propuseram, através do que ficou conhecido por mecanismo de Higgs, o uso da quebra espontânea de simetria para comportar massa nestas partículas. O mecanismo por sua vez prediz a existência de uma nova partícula, o bosão de Higgs. O bosão/bóson de Higgs foi detectado no LHC do CERN em Julho de 2012, com probabilidade maior que 5 sigmas de ser verdadeira tal identificação.
Uso na matemática
Na matemática o uso mais comum da quebra espontânea de simetria é pelo uso da Função de Lagrange, a qual essencialmente indica como um sistema irá se comportar por meio de termos potenciais
equação Graceli estatística tensorial quântica de campos
1 / / /
G
G [DR] = .=
+ G* = = [ ] ω , , / T] / c [ [x,t] ] =
//////
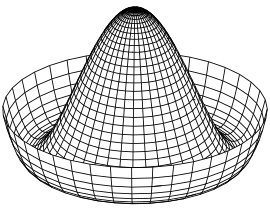
É neste termo potencial que a ação da quebra de simetria ocorre. Como demonstra o gráfico do chapéu mexicano
equação Graceli estatística tensorial quântica de campos
1 / / /
G
G [DR] = .=
+ G* = = [ ] ω , , / T] / c [ [x,t] ] =
//////
Este termo potencial possui vários possíveis mínimos dados por
equação Graceli estatística tensorial quântica de campos
1 / / /
G
G [DR] = .=
+ G* = = [ ] ω , , / T] / c [ [x,t] ] =
//////
para qualquer real no intervalo . Este sistema também possui um estado do vácuo quântico que corresponde ao , este estado possui um grupo unitário simétrico. Entretanto, uma vez que o sistema atinja um estado específico no vácuo (que corresponda a um valor para ) a simetria será espontaneamente quebrada.
Exemplos fora da Física
O fenômeno da quebra espontânea de simetria também é encontrado em Dinâmica de Tráfego de Veículos,[1] sistemas difusivos,[2] econômicos[3] e sociais.[4]
Uma força fundamental é um mecanismo pelo qual as partículas interagem mutuamente, e que não pode ser explicado por nenhuma força mais fundamental. Cada fenômeno físico observado, desde uma colisão de galáxias até quarks agitando-se dentro de um próton, pode ser explicado por estas interações. Devido a sua importância fundamental, a compreensão destas interações ocupou a atenção dos físicos por meio século e continua ocupando até hoje.
Tradicionalmente, o físico moderno tem listado 4 interações: gravidade, eletromagnetismo, a força nuclear fraca, e a força forte. Suas magnitudes e comportamentos variam muito, como pode ser visto na tabela abaixo. Ainda, existe uma crença muito forte de que 3 destas interações (eletromagnetismo, força nuclear fraca e força forte) sejam a manifestação de uma única interação, mais fundamental, tal como a eletricidade e o magnetismo são agora entendidos como dois aspectos de uma interação eletromagnética. Eletromagnetismo e forças nucleares fracas têm se mostrado como dois aspectos da força eletrofraca. De forma mais especulativa, a força eletrofraca e a força nuclear forte podem vir a ser combinadas usando as teorias da grande unificação. Como combinar a quarta interação, a gravidade, com as outras três ainda é um tópico para a pesquisa em gravitação quântica.
equação Graceli estatística tensorial quântica de campos
1 / / /
G
G [DR] = .=
+ G* = = [ ] ω , , / T] / c [ [x,t] ] =
//////
Teoria Interação mediador Magnitude relativa Comportamento Faixa Cromodinâmica Força nuclear forte Glúon 1041 1/r7 1,4 × 10-15 m Eletrodinâmica Força eletromagnética Fóton 1039 1/r2 infinito Flavordinâmica Força nuclear fraca Bósons W e Z 1029 1/r5 até 1/r7 10-18 m Geometrodinâmica Força gravitacional gráviton 10 1/r2 infinito Estas interações são algumas vezes chamadas de "forças fundamentais", embora muitos achem que esta terminologia seja enganosa porque uma delas, gravidade, não é totalmente explicada por uma "força" no sentido newtoniano: nenhuma "força gravitacional" está atuando à distância para levar um corpo a se acelerar (como era o que se acreditava até o século anterior com a teoria da gravitação newtoniana). Ao invés disto, a relatividade geral explicou a gravitação pela a curvatura do espaço-tempo (composta da dilatação gravitacional do tempo e da curvatura do espaço).
A visão da mecânica quântica moderna das três forças fundamentais (todas, exceto a gravidade) é que as partículas da matéria (férmions) não se interagem mutuamente mas pela troca de partículas virtuais (bósons) chamadas de condutores de interação ou mediadores de interação. Esta dupla de matéria (férmions) com as partículas mediadoras (bósons) são entendidas como sendo resultado de alguma simetria fundamental da natureza.
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
 /
/  /
/ 
 G
G 















![{\displaystyle {\mathcal {L}}={\bar {\psi }}_{B}\left[i\gamma _{\mu }\left(\partial ^{\mu }+ie_{B}A_{B}^{\mu }\right)-m_{B}\right]\psi _{B}-{\frac {1}{4}}F_{B\mu \nu }F_{B}^{\mu \nu }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/380fd2c0d942ca26fb6e07d41132bd041f98c187)













Comentários
Postar um comentário