MECÂNICA GRACELI - ESTATÍSTICA QUÂNTICA TENSORIAL DE CAMPOS [570]

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ [DR] = ${\hat {H}}$ $\left|\psi ({\vec {r}},t)\right\rangle$ $F^{\mu \nu }$ $T^{\mu \nu }$ $P^{\mu }\!$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$

$\psi ^{*}$

//////

A intensidade de cada interação é definida pela sua constante de acoplamento, um parâmetro adimensional que serve para comparar as diferentes interações. No caso particular da interação eletromagnética, a constante de acoplamento é obtida a partir da expressão da energia potencial eletrostática entre duas cargas puntiformes divida pelor fator ħc.

$V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$

A constante de acoplamento da interação eletromagnética é também conhecida como a constante de estrutura fina $\alpha \approx 1/137$ , já substituindo os valores das constantes. Na tabela a seguir são apresentadas características específicas de cada interação:[

A formulação de Feynman da mecânica quântica ou formulação de integrais de caminho da mecânica quântica é uma descrição da teoria quântica que generaliza a ação da mecânica clássica. Ela substitui a noção clássica de uma única trajetória para um sistema por uma soma, ou integral funcional, por meio de uma infinidade de trajetórias possíveis para calcular a amplitude quântica.

A ideia básica da formulação de integral de caminho é originária de Norbert Wiener, que apresentou o processo de Wiener para a solucionar problemas de difusão e movimento Browniano.^[1] Esta ideia foi estendida para o uso do Lagrangiana na mecânica quântica por P. A. M. Dirac em seu artigo de 1933^[2] . O método completo foi desenvolvido em 1948 por Richard Feynman. Algumas preliminares foram trabalhados anteriormente, no curso de sua tese de doutorado no trabalho de John Archibald Wheeler. A motivação original surgiu da aspiração de obter uma formulação da mecânica quântica para a teoria de teoria de ação à distância de Wheeler e Feynman usando uma Lagrangeana (ao invés de um Hamiltoniano) como ponto de partida.

Esta formulação tem se provado fundamental para o desenvolvimento posterior da física teórica, por ser manifestamente simétrica entre o tempo e o espaço. Ao contrário dos métodos anteriores, a formulação de integral de caminho-integral permite facilmente a mudança de coordenadas entre descrições canônicas diferentes do mesmo sistema quântico.

A formulação de integral de caminho também relaciona processos quânticos e estocásticos, fornecendo a base para a grande síntese, na década de 1970 que unificou a teoria quântica de campos com a teoria de campos estatísticos de campo flutuante perto de uma transição de fase de segunda ordem. A equação de Schrödinger é uma equação de difusão com uma constante de difusão imaginária, sendo a integral de caminho uma continuação analítica do método para a soma de todos as possíveis caminhadas aleatórias. Por esta razão integrais de caminho foram utilizados no estudo de difusão e movimento Browniano pouco antes de serem introduzidos na mecânica quântica.^[3]

Estes são apenas três dos caminhos que contribuem para amplitude quântica de uma partícula movendo-se do ponto A em tempo t₀ para o ponto B em t₁.

Princípio da ação quântica

Na mecânica quântica, assim como na mecânica clássica, o Hamiltoniano é o gerador de translações temporais. Isto significa que o estado em um tempo posterior difere do estado atual pela atuação do operador Hamiltoniano (multiplicado pelo negativo unidade imaginária, −i). Para os estados com uma determinada energia, esta é uma instrução de relação de De Broglie entre a frequência e a energia, e a relação geral é consistente com o que e o princípio da superposição.

No entanto, na mecânica clássica o Hamiltoniano é derivado a partir de um Lagrangeana, que é uma quantidade mais fundamental em relação à relatividade especial. O Hamiltoniano indica como o movimento se desenvolve no tempo, mas o tempo é diferente em diferentes sistemas de referência. Assim, o Hamiltoniano é diferente em referenciais diferentes e este tipo de simetria não é aparente na formulação original da mecânica quântica.

O hamiltoniano é uma função da posição e momento no tempo t, determinando a posição e o momento no tempo (t+ε). A Lagrangiana é uma função das posição em t e (t+ε) (para um intervalo de tempo infinitesimal, a velocidade é medida é a velocidade instantânea, tornando a Lagrangeana como função da posição e da velocidade). A relação entre os dois é por uma transformação de Legendre e a condição que determina as equações de movimento (ou equações de Euler–Lagrange) é a extremização da ação.

Na mecânica quântica, uma transformação de Legendre é difícil de interpretar uma vez que o movimento não é dado por uma trajetória definida. Na mecânica clássica, a discretização temporal da transformação de Legendre torna-se:

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

\epsilon H=p(t)(q(t+\epsilon )-q(t))-\epsilon L\,

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

p={\partial L \over \partial {\dot {q}}}\,

onde a derivada parcial com relação a mantém q(t + ε) constante. A inversa da transformação de Legendre é:

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

\epsilon L=\epsilon p{\dot {q}}-\epsilon H\,

onde

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

{\dot {q}}={\partial H \over \partial p}\,

tomando q fixo.

Na mecânica quântica, um estado qualquer é uma superposição de estados independentes, com diferentes valores de q, ou diferentes valores de p, sendo que o momento e a posição (p e q) podem ser interpretadas como operadores que não comutam. O operador p é definitivo em estados onde q são indeterminados. Considere dois estados separados no tempo. A atuação do operador correspondente à Lagrangiana:

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

e^{i(p(q(t+\epsilon )-q(t))-\epsilon H(p,q))}\,

Se a multiplicação implícita na fórmula são reinterpretados como multiplicação de matrizes, o primeiro fator é:

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

e^{-ipq(t)}\,

Se esse também é interpretado como uma multiplicação de matrizes, a soma sobre todos os estados integra todos q(t), levando a transformada de Fourier em q(t), mudando a base para p(t). Isto é a ação sobre o espaço de Hilbert – mudar de base para p no tempo t.

Em seguida, tem-se:

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

e^{-i\epsilon H(p,q)}\,

que é uma evolução infinitesimal para o futuro.

Finalmente, o último fator, nessa interpretação, é:

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

e^{ipq(t+\epsilon )}\,

que é uma mudança de base de volta para q no tempo (t+ε).

Isto não é diferente do operador de evolução temporal: o fator H contém toda informação da dinâmica, avançando o estado no tempo. A primeira e a última parte são as transformadas de Fourier para a mudança na base pura de q a partir de uma base intermediária p.

De forma equivalente, pode-se dizer que: uma vez que o Hamiltoniano é naturalmente uma função de p e q, exponenciando estas quantidades e realizando uma mudança de base de p para q em cada passo permite expressar o elemento da matriz de H como uma função simples ao longo de cada caminho. Esta função é o análogo quântico da ação clássica. Esta observação é feita por Paul Dirac.

Dirac observou ainda que se pudesse, o quadrado do tempo-a evolução do operador no S representação:

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

e^{i\epsilon S}\,

e isso é o operador de evolução temporal entre o tempo t e o tempo t + 2ε. Enquanto que na representação H a quantidade que está sendo somada nos estados intermediários é um elemento de matriz obscuro, na representação S esta é reinterpretado como uma quantidade associada ao caminho. No limite que leva um grande poder de esse operador, reconstrói-se a evolução quântica completa entre dois estados sendo o estada mais antigo com valor fixo q(0) a o estado mais recente com valor q(t). O resultado é uma soma sobre os caminhos com uma fase que é a ação quântica. Crucialmente, Dirac identificada neste papel, a profundidade da mecânica quântica razão do princípio da mínima ação de controlar o limite clássico.

Na física teórica, especificamente na teoria quântica de campos, uma função beta, β(g), codifica a dependência de um parâmetro de acoplamento, g, na escala de energia, μ, de um determinado processo físico descrito pela teoria quântica de campos.^[1] É definido como

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

\beta (g)={\frac {\partial g}{\partial \log(\mu )}}~,

^[2]

e, por causa do grupo de renormalização subjacente, ele não tem dependência explícita de μ, portanto, depende apenas de μ implicitamente por meio de g. Essa dependência da escala de energia assim especificada é conhecida como a execução do parâmetro de acoplamento, uma característica fundamental da dependência de escala na teoria quântica de campos, e sua computação explícita pode ser alcançada por meio de uma variedade de técnicas matemáticas.^[3]

Em teoria quântica de campo, a função de correlação de n pontos é definida como a média funcional (valor esperado funcional) de um produto de $�$ operadores de campo em posições diferentes

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

C_{n}\left(x_{1},x_{2},\ldots ,x_{n}\right):=\left\langle \phi (x_{1})\phi (x_{2})\cdots \phi (x_{n})\right\rangle ={\frac {\int {\mathcal {D}}\phi \;e^{-S[\phi ]}\phi (x_{1})\cdots \phi (x_{n})}{\int {\mathcal {D}}\phi \;e^{-S[\phi ]}}}

Para funções de correlação dependentes do tempo, é necessário incluir o operador de ordenação temporal, $�$ .

O termo função de Green é certas vezes generalizado para descrever qualquer função de correlação de n pontos, em vez de apenas funções de dois pontos.

A função de correlação de dois pontos pode ser interpretada fisicamente como a amplitude de propagação de uma partícula ou excitação entre dois pontos no espaço-tempo. Na teoria livre, esta corresponde simplesmente ao propagador de Feynman.^[1]

A função de partição é, em mecânica estatística, uma grandeza que descreve as propriedades estatísticas de um sistema em equilíbrio termodinâmico. É uma função da temperatura e outros parâmetros, tais como o volume de enclausuramento de um gás. As variáveis termodinâmicas do sistema, tais como a energia total, energia livre, entropia, e pressão, são expressas em termos da funçao de partição do sistema, mas a sua determinação explícita pode ser extremamente complexa em alguns casos.

Existem várias formas de funções de partição, cada qual correspondendo a diferentes tipos de ensemble estatístico (ou, equivalentemente, diferentes tipos de energia livre.) A função de partição canônica aplica-se ao ensemble canônico, no qual o sistema esta sujeito a trocar calor com o ambiente a temperatura fixa, volume, e número de partículas. A grande função partição canônica aplica-se ao ensemble grande canônico, no qual o sistema pode trocar tanto calor e partículas com o ambiente, a temperatura, volume, e potencial químico fixos. Outros tipos de funções de partição podem ser definidas para diferentes circunstâncias.

Função de partição canônica

Definição

Consideremos um sistema termodinamicamente grande que está em contato térmico com o ambiente, que fixa a temperatura T, com ambos o volume do sistema e o número de partículas constituintes fixas. Este tipo de sistema é chamado de ensemble canônico. Deixemo-nos rotulá-lo com os estados (micro-estados) exatos que podem ocupar por j (j = 1, 2, 3, ...), e denominar a energia total do sistema quando está no micro-estado j como E_j. Geralmente, estes micro-estados podem ser considerado como discretos estados quânticos do sistema.

A função de partição canônica é ^[1]

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

Z=\sum _{j}e^{-\beta E_{j}}

onde a "temperatura inversa" β é convenientemente definida como

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

\beta \equiv {\frac {1}{k_{B}T}}

com k_B denotando a constante de Boltzmann. Algumas vezes a degenerescência dos estados é também usada e a a função de partição se escreve

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

Z=\sum _{j}g_{j}\cdot e^{-\beta E_{j}}

onde $g_{j}$ é o grau de degenerescência do auto-estado de energia $E_{j}$ .

Em mecanismos estatísticos clássicos não é realmente correto expressar a função de partição como uma soma de termos discretos, como estamos fazendo. Em mecânica clássica, as variáveis posição e momento de uma partícula podem variar continuamente, então o conjunto de micro-estados é então não enumerável. Neste caso, algum formas de tratamento grosseiro da granuralidade devem ser realizados, que atinge essencialmente o tratamento de dois estados mecânicos como o mesmo micro-estado se as diferenças em suas variáveis da posição e do momento forem "não demasiado grandes". A função de partição então toma a forma de uma integral. Por exemplo, a função de partição de um gás de N partículas clássicas é

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

Z={\frac {1}{N!\,h^{3N}}}\int \,\exp[-\beta H(p_{1}\cdots p_{N},x_{1}\cdots x_{N})]\;\mathrm {d} ^{3}p_{1}\cdots \mathrm {d} ^{3}p_{N}\,\mathrm {d} ^{3}x_{1}\cdots \mathrm {d} ^{3}x_{N}

$p_{i}$ indicam os momentos das partículas
$x_{i}$ indicam as posições das partículas
$d^{3}$ é uma porção de notação de estenografia como lembrete que $p_{i}$ e $x_{i}$ são vetores em um espaço tridimensional

onde h é alguma quantidade infinitesimal com unidades de ação (usualmente tomadas como sendo a constante de Planck, de maneira a ser consistente com a mecânica quântica), e H é a clássica Hamiltoniana. A razão para o fator N! é discutido abaixo. Por simplificação, usaremos a forma discreta da função de partição neste artigo, mas nossos resultados irão aplicar-se igualmente bem à forma contínua.

Em mecânica quântica, a função de partição pode ser formalmente escrita como o traço sobre a espaço de estado:

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

Z=\operatorname {tr} (e^{-\beta H})

onde H é o operador Hamiltoniano quântico. O exponencial de um operador pode ser definido, para considerações puramente físicas, usando séries de potências exponenciais.

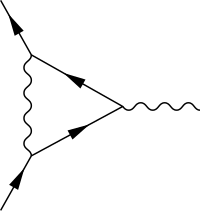
Na eletrodinâmica quântica, a função de vértice descreve o acoplamento entre um fóton e um elétron além da ordem principal da teoria das perturbações.^[1]^[2] Em particular, é a função de correlação irredutível de uma partícula envolvendo o férmion $\psi$ , o antifermion ${\bar {\psi }}$ e o potencial vetorial A.^[3]^[4]

Definição

A correção de um loop para a função de vértice. Esta é a contribuição dominante para o momento magnético anômalo do elétron.

A função de vértice $\Gamma ^{\mu }$ pode ser definida em termos de uma derivada funcional^[5] da ação efetiva S_eff as

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

\Gamma ^{\mu }=-{1 \over e}{\delta ^{3}S_{\mathrm {eff} } \over \delta {\bar {\psi }}\delta \psi \delta A_{\mu }}

A contribuição dominante (e clássica) para $\Gamma ^{\mu }$ é a matriz gama $\gamma ^{\mu }$ , o que explica a escolha da letra. A função de vértice é restringida pelas simetrias da eletrodinâmica quântica — Invariância de Lorentz; invariância de calibre ou transversalidade do fóton, conforme expresso pela identidade de Ward; e invariância sob paridade - para assumir a seguinte forma:

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

\Gamma ^{\mu }=\gamma ^{\mu }F_{1}(q^{2})+{\frac {i\sigma ^{\mu \nu }q_{\nu }}{2m}}F_{2}(q^{2})

onde $\sigma ^{\mu \nu }=(i/2)[\gamma ^{\mu },\gamma ^{\nu }]$ , $q_{\nu }$ é o quadrimomento de entrada do fóton externo (no lado direito da figura), e F₁(q²) e F₂(q²) são fatores de forma^[6] que dependem apenas da transferência de momento q². No nível da árvore (ou ordem inicial), F₁(q²) = 1 e F₂(q²) = 0. Além da ordem inicial, as correções para F₁(0) são exatamente cancelados pela renormalização da intensidade do campo.^[7]^[8] O fator de forma F₂(0) corresponde ao momento magnético anômalo^[9]^[10] a do férmion, definido em termos do fator g de Landé^[11]^[12] como:

$equação Graceli estatística tensorial quântica de campos$

$1 /$ $\psi ^{*}$ $V(r)={\frac {U(r)}{\hbar c}}=-{\frac {e^{2}}{4\pi \epsilon _{0}\hbar c}}{\frac {1}{r}}$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $P^{\mu }\!$

$\psi ^{*}$

//////

a={\frac {g-2}{2}}=F_{2}(0)

Pesquisar este blog

MECÂNICA GRACELI - ESTATÍSTICA QUÂNTICA TENSORIAL DE CAMPOS [570]

Princípio da ação quântica

Função de partição canônica

Definição

Definição

Comentários

Postar um comentário

Postagens mais visitadas deste blog